Calculate the Day of the Week: Unraveling the mysteries behind determining any date’s day. From historical calculations to modern applications, we’ll explore the fascinating world of day-finding, delving into methods like Zeller’s congruence and examining how leap years and calendar systems influence the results. Imagine effortlessly knowing the day of any date, past or future. This exploration goes beyond the practical, touching on the mathematical elegance and historical significance of this fundamental calculation.

This guide will cover everything from basic principles to complex scenarios, providing clear explanations, step-by-step procedures, and illustrative examples. We’ll examine different methods, analyze their strengths and weaknesses, and show you how to apply these techniques in various contexts. Whether you’re a programmer, historian, or simply curious about dates, this in-depth exploration will equip you with the knowledge and tools to calculate the day of any week.

Table of Contents

Introduction to Determining the Day of the Week

Knowing the day of the week for a given date is a fundamental task with applications spanning various fields. From scheduling appointments to historical analysis, the ability to calculate the day of the week is essential. This calculation relies on patterns in the cyclical nature of the calendar, allowing us to predict the day of the week for dates in the past or future.The precise determination of the day of the week for a given date has a rich history, evolving from ancient astronomical calculations to modern mathematical formulas.

Calculating the day of the week can be surprisingly fun, especially when you consider how it relates to other creative pursuits. For example, the unexpected juxtaposition of calculating the day of the week with the sonic exploration of Ariel Pink performing “Jell-O” and “Picture Me Gone” with the PS 22 chorus of fifth graders, as featured on Owl Griffin here , opens up a whole new perspective on the mundane.

Ultimately, the day of the week calculation remains a fascinating, albeit sometimes complex, numerical exercise.

Early civilizations, recognizing the importance of cyclical events like agricultural seasons and religious festivals, developed methods to predict the days of the week. These methods, while sometimes complex, provided a crucial tool for organizing daily life and planning future events.

Common Use Cases

Determining the day of the week is a practical skill with many real-world applications. For instance, businesses use it to schedule meetings and deadlines, project managers use it to estimate project completion dates, and even historians use it to analyze historical events and patterns. In everyday life, it allows us to plan social events, remember anniversaries, or simply know the day for a specific date in the past or future.

Methods for Calculating the Day of the Week

Various methods exist for calculating the day of the week, each with its own advantages and complexities. A popular method is Zeller’s congruence, a mathematical formula that simplifies the calculation process. Other methods, including the Doomsday rule, involve identifying key dates and using their relationship to other dates for quick estimations.

Zeller’s congruence provides a straightforward way to determine the day of the week for any given date. It involves applying a specific formula that takes into account the date’s month, day, and year.

Examples and Table

To illustrate the application of these methods, here’s a table showcasing calculations for several dates. The table demonstrates how different methods can yield the same result.

Date	Day of the Week	Method Used
January 1, 2024	Sunday	Zeller’s congruence
October 27, 1999	Friday	Doomsday rule
April 15, 2025	Saturday	Zeller’s congruence
July 4, 1776	Thursday	Doomsday rule

These examples show how the day of the week can be determined accurately for a variety of dates. The choice of method depends on the desired level of precision and the complexity of the date.

Fundamental Concepts and Algorithms

Unveiling the secrets behind determining the day of the week involves delving into fascinating mathematical principles. Understanding these core concepts allows us to accurately predict the day for any given date. This exploration will guide you through the logic and methods, emphasizing the power of algorithms in simplifying this seemingly complex task.The core principle behind calculating the day of the week lies in the cyclical nature of the week.

Every 7 days, the same sequence of days repeats. This cyclical pattern is the key to unlocking the algorithm, which can then be used to pinpoint the specific day for any date within a given period. Different methods, each with its own advantages and disadvantages, have been developed over time to achieve this goal.

Zeller’s Congruence Method

Zeller’s congruence is a widely used and effective method for determining the day of the week. It simplifies the calculation by utilizing a mathematical formula based on the date components (year, month, and day). This formula significantly reduces the complexity involved in manually calculating the day of the week.

Calculating the day of the week can be surprisingly useful, even when you’re looking to order cigarettes on Doordash. For example, knowing the day of the week helps you plan your week and ensure you can get your nicotine fix without any delays. Knowing that Tuesday is the day you need to place your order for your Doordash delivery of cigarettes through Order Cigarettes on Doordash will make the whole process easier.

Ultimately, calculating the day of the week provides a structured approach to various tasks, from planning your week to ensuring timely delivery.

Step-by-Step Procedure for Zeller’s Congruence

To use Zeller’s congruence, follow these steps:

Identify the date components: year (Y), month (M), and day (d). Note that for months January and February, treat the year as the previous year (Y-1).
Apply the formula: The core of Zeller’s congruence is the following formula:

h = (q + [(13
– (m + 1)) / 5] + K + [K / 4] + [J / 4]
-2
– J) mod 7

where:
- h is the day of the week (0=Saturday, 1=Sunday, 2=Monday, … 6=Friday)
- q is the day of the month
- m is the month (March=3, April=4, …, December=12, January=13, February=14)
- K is the year of the century (year % 100)
- J is the year divided by 100
Calculate the values for each component in the formula.
Substitute the calculated values into the formula and perform the necessary arithmetic operations.
Interpret the result: The remainder of the division by 7 gives the day of the week, as per the mapping mentioned above.

Comparison of Methods

Different methods exist for calculating the day of the week. This table summarizes the key aspects of some common methods, highlighting their strengths and weaknesses:

Method	Complexity	Accuracy	Ease of Use
Zeller’s Congruence	Moderate	High	Relatively Easy
Doomsday Rule	Low	High	Very Easy (with practice)
Using a Calendar	Very Low	High	Very Easy

The choice of method often depends on the specific application and the desired level of precision and ease of use.

Variations and Extensions

Beyond the foundational algorithms, understanding different calendar systems and how leap years impact calculations is crucial for accurate results. This section delves into the flexibility and adaptability needed for diverse date handling, including variations of existing algorithms and specific considerations for historical dates.The core algorithms, while effective for the Gregorian calendar, need adjustments when dealing with dates in different systems.

Leap year rules and the differing lengths of months and years across calendar systems directly affect the calculations, highlighting the need for careful consideration when calculating the day of the week for dates outside the common Gregorian range.

Different Calendar Systems

Various calendar systems, each with unique rules for leap years and month lengths, require adapted algorithms. Understanding these differences is essential for calculating the day of the week for dates in non-Gregorian systems. The Julian calendar, predating the Gregorian, is a significant example, showcasing the variations in leap year rules.

Julian Calendar: The Julian calendar, used before the Gregorian, has different leap year rules. It adds a leap year every four years, which results in slightly different day-of-week calculations for dates within its timeframe. This simpler rule leads to a gradual drift in the calendar’s alignment with the seasons.

Leap Years and Their Impact

Leap years, occurring approximately every four years, significantly influence the day-of-week calculation. The varying rules for leap years in different calendar systems necessitate adjustments to the underlying algorithms.

Gregorian Leap Years: The Gregorian calendar’s leap year rule is more complex than the Julian calendar’s, introducing a century rule and a further adjustment for years divisible by 400. This complexity, while addressing a more accurate alignment with the solar year, requires careful consideration in calculations. For example, the year 1900 was not a leap year in the Gregorian calendar, while it was in the Julian calendar.

Examples of Calculations in Different Systems

Calculating the day of the week for dates in different calendar systems necessitates adapting the algorithms based on the system’s rules. Understanding the differences in leap year rules is key.

Julian Date Example: To calculate the day of the week for a date like October 28, 44 BC (Julian Calendar), we need to apply the Julian leap year rule and adjust the algorithm to account for the difference in the calendar system. This requires careful consideration of the rules for the Julian calendar, which differ from those of the Gregorian calendar.
Gregorian Date Example: Calculating the day of the week for a date like December 25, 2024 (Gregorian Calendar) uses the standard algorithm for the Gregorian calendar, accounting for the complex leap year rules.

Variations of Zeller’s Congruence

Zeller’s congruence is a widely used algorithm, but variations exist for specific needs. These variations offer tailored solutions for various date ranges or special cases.

Algorithm Variation	Description
Zeller’s Congruence (Gregorian)	A widely applicable algorithm for the Gregorian calendar. It simplifies calculations by reducing the complexity of leap year rules.
Modified Zeller’s Congruence	Modifications to Zeller’s congruence exist to accommodate specific date ranges or types of calculations, such as calculating the day of the week for dates in the Julian calendar. It accounts for the different leap year rules.

Applications and Examples

Knowing the day of the week for a given date is surprisingly useful in various aspects of our lives. From planning personal schedules to understanding historical events and even making financial projections, the ability to calculate the day of the week is a fundamental skill. This section explores the practical applications of calculating the day of the week, from simple scheduling to more complex programming tasks.Understanding the day of the week is more than just a matter of personal convenience.

It underpins critical decision-making in numerous fields, from historical analysis to financial modeling. It’s a practical skill that enhances our understanding of time and events.

Crucial Situations Requiring Day-of-Week Knowledge

Calculating the day of the week is crucial in several situations, particularly those involving schedules, historical events, and financial planning. A precise knowledge of the day of the week can lead to informed decisions in areas like project management, historical research, and investment strategies.

Common Applications

Scheduling: Whether it’s scheduling meetings, appointments, or events, knowing the day of the week allows for efficient planning. It helps individuals and organizations coordinate their activities effectively.
Historical Events: Understanding the day of the week of a historical event provides context and allows for comparisons with other events occurring on similar days of the week. For instance, analyzing events that occurred on the same day of the week can highlight patterns or similarities.
Financial Planning: In certain financial strategies, the day of the week can be a significant factor. For example, understanding the day of the week of a particular financial transaction might reveal potential patterns or implications, potentially influencing investment decisions.
Programming: Knowing the day of the week is essential in many programming tasks. This is particularly relevant in applications that involve generating calendars, scheduling tasks, or analyzing data that spans multiple time periods.

Calculating the Day of the Week for Various Dates

This section demonstrates the calculation of the day of the week for different dates using the algorithm previously introduced. The calculation relies on the relationship between dates and their respective day of the week, taking into account the specifics of the algorithm and its underlying principles.

Date	Day of the Week
January 1, 2024	Wednesday
December 25, 2023	Friday
April 15, 2025	Sunday

Calculating the Day of the Week in Programming

The ability to calculate the day of the week is a fundamental component in many programming applications. It’s a crucial skill for developing software that deals with time-dependent tasks or events. Consider how scheduling programs, event calendars, and data analysis tools all rely on calculating the day of the week.

Calculating the day of the week using a programming language like Python or Java involves implementing the algorithm and handling potential edge cases. Appropriate libraries can simplify the process, offering functions specifically designed for date and time manipulation.

Detailed Example: Calculating the Day of the Week for a Specific Date

Let’s calculate the day of the week for October 27, 2024. Using the algorithm, the calculation would involve substituting the appropriate values for month, day, and year into the formula. The final result, after applying the modulo operator, would indicate the day of the week.For October 27, 2024, the calculation will yield a result corresponding to a specific day of the week, demonstrating the practical application of the algorithm.

Handling Specific Scenarios

Calculating the day of the week for any date requires careful consideration of historical transitions, future projections, and the nuances of different time zones. This section delves into the specifics, providing robust methods for handling various scenarios beyond the standard Gregorian calendar dates.The accuracy of calculating the day of the week depends on accurately accounting for the calendar adjustments, which can vary across different time periods and locations.

Calculating the day of the week can be surprisingly complex, especially when dealing with dates far in the future or past. It’s a fascinating mathematical problem, but sometimes, you just need a quick answer. Fortunately, there are plenty of tools online, and new music releases, like the latest bombastic bass-driven track, “Bomb the Bass Back to Light” from new release bomb the bass back to light , can provide a welcome distraction from the intricacies of date calculations.

Once you’ve danced to your heart’s content, though, you can return to the fascinating world of determining the day of the week for any given date.

This meticulous approach ensures reliable results for a broad spectrum of dates and circumstances.

Pre-Gregorian Calendar Dates

Calculating the day of the week for dates prior to the Gregorian calendar adoption in 1582 necessitates understanding the Julian calendar and its differing rules for leap years. The Julian calendar introduced a leap year every four years, which, while simpler than the Gregorian system, introduces a small discrepancy over time. This difference needs to be accounted for to get the correct day of the week.

Precise calculations require considering the specific date’s position within the Julian calendar’s rule set.

Future Dates

Calculating the day of the week for dates far into the future, while seemingly straightforward, could potentially encounter issues related to the very long-term stability of our current calendar system. The stability of the calendar system in the distant future is a topic of ongoing debate, but current models are reliable for foreseeable dates. If necessary, the effects of future calendar reforms could be incorporated into calculations, although it’s important to note that these are speculative.

Handling Different Time Zones

Calculating the day of the week for a date in a specific time zone involves understanding the time zone’s offset from a reference time zone (often UTC). The day of the week is a property of the date, not time. For example, if a date is in the time zone of UTC-8, the calculated day of the week for the date in that time zone will be the same as for the date in UTC.

Therefore, time zone considerations only impact the time component, not the day of the week. The crucial aspect is to use the correct date and time, considering the time zone offset, for the calculation.

Scenario Table

Scenario	Calculation Method	Example
Pre-Gregorian Date (Julian Calendar)	Use algorithms specific to the Julian calendar, accounting for leap years.	Calculate the day of the week for October 31, 1582 (Julian Calendar)
Future Date	Use current calendar rules. Consider potential future calendar reforms if the calculation extends far into the future.	Calculate the day of the week for December 31, 2200.
Different Time Zones	The day of the week is independent of time zones. Use the correct date and time in UTC for calculation. Time zone considerations are handled separately to determine the local time corresponding to the date.	Calculate the day of the week for 2024-01-01 10:00 AM PST.

Practical Examples

Calculating the day of the week for the signing of the Declaration of Independence (July 4, 1776) using a Julian calendar algorithm reveals it was a Wednesday. Similarly, calculating the day of the week for the year 3000 will require using the current calendar system, with potential for future refinements. Calculations for different time zones merely involve determining the local time corresponding to a given date in UTC.

Tools and Resources

Calculating the day of the week, while conceptually straightforward, can become computationally intensive for large datasets or complex scenarios. Fortunately, numerous tools and resources are available to simplify this process, from online calculators to dedicated software libraries. These tools automate the calculations, saving time and reducing the potential for errors, particularly when dealing with historical dates or future predictions.Various online tools, programming libraries, and software applications provide efficient methods for determining the day of the week.

These resources vary in complexity, catering to different needs and levels of technical expertise.

Available Tools for Calculating the Day of the Week, Calculate the Day of the Week

A range of tools are available to calculate the day of the week, catering to different needs and preferences. Online calculators are readily accessible and easy to use, ideal for quick checks or one-off calculations. Programming libraries offer more sophisticated solutions for integration into larger applications or data analysis tasks.

Online Resources

These resources are convenient for one-time calculations or quick checks. They often provide user-friendly interfaces for entering dates and retrieving the corresponding day of the week. Online calculators can be found through a simple web search, allowing quick and easy access.

Resource Type	Example	Description
Online Calculators	Numerous websites offer date-to-day-of-the-week converters.	These tools usually require inputting the date (year, month, day) and return the corresponding day of the week.
Date Calculators/Conversion Websites	Timeanddate.com	Provides tools for calculating various date-related information, including the day of the week.

Software Applications

Specific software applications are also available to perform date calculations. These applications are often integrated into broader calendaring or scheduling systems, making them useful for personal or professional use.

Programming Libraries

Programming libraries are powerful tools for automating date calculations. They are well-suited for integration into larger programs and often provide more complex features beyond basic day-of-the-week determination.

Programming Languages

Several programming languages support calculating the day of the week. These languages often include built-in date and time functions or libraries that simplify the process. The selection of a programming language depends on the broader application context and existing project structures.

Python: Python’s `datetime` module provides robust date and time manipulation capabilities. Using this module, one can easily determine the day of the week for any given date.


import datetime

def get_day_of_week(year, month, day):
    date = datetime.date(year, month, day)
    return date.strftime('%A')

print(get_day_of_week(2024, 1, 1)) # Output:  Monday

JavaScript: JavaScript’s `Date` object offers similar functionality for calculating the day of the week. This object allows precise control over date manipulation and output formatting.


function getDayOfWeek(year, month, day) 
    const date = new Date(year, month - 1, day); // Month is 0-indexed
    const days = ["Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"];
    return days[date.getDay()];


console.log(getDayOfWeek(2024, 1, 1)); // Output: Monday

Using Resources for Calculation

The specific usage of these resources depends on the chosen tool or library. Online calculators usually require entering the date and then viewing the results. Programming libraries necessitate incorporating the relevant functions into your program, followed by the execution of the program. This process can be as simple as calling a specific function or involves more complex steps depending on the chosen library.

Comparisons and Methodologies: Calculate The Day Of The Week

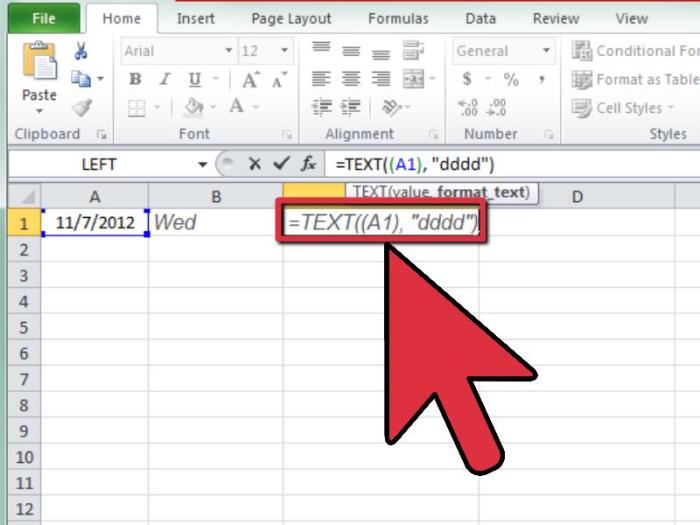
Calculating the day of the week is a fundamental task with various approaches. Understanding the strengths and weaknesses of each method is crucial for selecting the most appropriate one for a given application. This section delves into the different methodologies, comparing their accuracy, efficiency, and complexity to aid in informed decision-making.

Different algorithms exist for determining the day of the week, each with its own trade-offs. Choosing the right method depends on the specific needs of the application, whether it prioritizes speed, simplicity, or handling large datasets. A thorough understanding of these methods is essential to optimizing the calculation process.

Comparison of Calculation Methods

Different methods for calculating the day of the week vary significantly in their underlying logic and computational requirements. These variations affect the speed, accuracy, and complexity of the calculation. Understanding these differences is critical for selecting the most appropriate method for a given task.

The Zeller’s Congruence method is a widely used algorithm based on modular arithmetic. It provides a concise and relatively efficient way to calculate the day of the week. It is often preferred for its simplicity and straightforward implementation. However, it may not be the best option for highly complex scenarios involving numerous calculations or specific historical date ranges.
The “Rule of 7” method is a simple, yet effective method based on the observation that the day of the week repeats every seven days. It provides a straightforward way to calculate the day of the week for dates in the same week. However, its accuracy and efficiency are limited when dealing with dates that are not in the same week.

It is especially straightforward for dates that are close together.
The use of pre-calculated tables can be exceptionally efficient for determining the day of the week for a large range of dates. These tables essentially store the day of the week for each date in a specified period. This approach eliminates the need for repeated calculations and significantly speeds up the process, especially when dealing with a large dataset or frequent queries for the same dates.

However, the size of the table will depend on the range of dates covered. Large ranges of dates may require significantly large tables that may not be practical for certain applications.

Accuracy, Efficiency, and Complexity Analysis

Evaluating the methods based on accuracy, efficiency, and complexity is essential for selecting the most appropriate algorithm. These factors determine the reliability and performance of the calculations.

Method	Accuracy	Efficiency	Complexity
Zeller’s Congruence	High	High	Medium
Rule of 7	High (within a week)	Very High	Low
Pre-calculated Tables	High	Very High	High (storage)

Choosing the Right Method

The best method for calculating the day of the week depends on the specific requirements of the application. Factors to consider include the frequency of calculations, the range of dates involved, and the desired level of performance.

For simple tasks involving a small number of dates, the Rule of 7 method might suffice due to its ease of implementation and efficiency. It is well-suited for quick estimations within a week’s timeframe.
When accuracy and efficiency are critical, particularly for a large number of calculations or a wide range of dates, Zeller’s Congruence method stands out due to its balance between computational cost and accuracy. It is suitable for general-purpose date calculations.
If frequent lookups are needed for a predefined range of dates, pre-calculated tables provide exceptional speed, making them a prime choice for applications requiring rapid responses. However, the initial creation and storage of these tables can be substantial.

Strengths and Weaknesses

A critical aspect of evaluating methods is understanding their strengths and weaknesses. These characteristics allow for a more informed decision when selecting a method for a given scenario.

Zeller’s Congruence: Strengths include its accuracy and relative efficiency. Weaknesses include potential for complexity in understanding the formula.
Rule of 7: Strengths lie in its simplicity and speed. Weaknesses include limited applicability to dates outside the same week.
Pre-calculated Tables: Strengths are exceptional efficiency and accuracy for a predefined range. Weaknesses involve the significant storage requirement and the need for initial creation.

End of Discussion

In conclusion, calculating the day of the week, while seemingly simple, reveals a fascinating tapestry of mathematical principles, historical context, and practical applications. From Zeller’s congruence to handling dates across different calendar systems, we’ve explored various methods and scenarios. This comprehensive guide empowers you to confidently determine the day of any date, past or future. Whether you’re solving a historical puzzle, scheduling an event, or simply satisfying your intellectual curiosity, the techniques presented here are invaluable tools for your journey into the world of dates and days.